So here is what I have done. Homogeneous has several meanings, but when I use it in this post, I will mean homogeneous functions. We only care about functions of two variables, so I will also only talk about them. A function 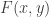 is called homogeneous of order
is called homogeneous of order  if
if  for some
for some  . Also, if we “pull” an
. Also, if we “pull” an  out, we get
out, we get 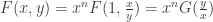 , which is why the definition is often stated that the function can be written as a function of
, which is why the definition is often stated that the function can be written as a function of  . Of course, we could do the same with
. Of course, we could do the same with  and get a function of
and get a function of  . Here is an example of a homogeneous function:
. Here is an example of a homogeneous function: 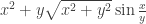 . You can see that
. You can see that 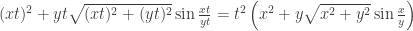 .
.
Now, if the coefficients  and
and  in the first order differential equation
in the first order differential equation 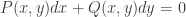 are both homogeneous functions of the same order, then the substitution
are both homogeneous functions of the same order, then the substitution  or
or 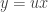 will make the equation separable. I will show how to do it for
will make the equation separable. I will show how to do it for 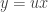 . We have
. We have 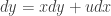 by the product rule. We also have
by the product rule. We also have  and
and 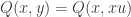 . Because these functions are homogeneous, we can “pull out” an
. Because these functions are homogeneous, we can “pull out” an 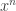 from each, giving us
from each, giving us 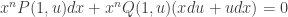 . Because we made the substitution
. Because we made the substitution 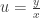 , we already have had to assume
, we already have had to assume 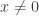 . Thus, we can divide the whole thing by
. Thus, we can divide the whole thing by 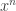 . Doing this, and expanding the remaining terms, we get
. Doing this, and expanding the remaining terms, we get 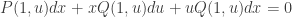 . Refactoring the
. Refactoring the 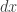 and
and 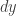 terms, we get
terms, we get  . The equation is separable! Separating variables and integrating, we get
. The equation is separable! Separating variables and integrating, we get  . If we had used
. If we had used  instead, we would have gotten
instead, we would have gotten 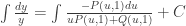 . This is exactly how I was able to solve these equations in SymPy. Each homogeneous equation has two possible integrals, and often the right hand side of one equation is a much harder integral than the right hand side of the other. Therefore, I did them both, and applied a little heuristic on which one to return. It prefers expressions that can be solved for y (f(x) in the case of SymPy), expressions that have evaluated integrals, and if neither of them are solvable, the shortest one, which tends to be the simplest.
. This is exactly how I was able to solve these equations in SymPy. Each homogeneous equation has two possible integrals, and often the right hand side of one equation is a much harder integral than the right hand side of the other. Therefore, I did them both, and applied a little heuristic on which one to return. It prefers expressions that can be solved for y (f(x) in the case of SymPy), expressions that have evaluated integrals, and if neither of them are solvable, the shortest one, which tends to be the simplest.
Here is an example from my text book.  . Astute readers of this blog may have noticed that this equation is exact. It is easier to solve that way, but we will try using the methods outlined above. First, we notice that the coeficients of
. Astute readers of this blog may have noticed that this equation is exact. It is easier to solve that way, but we will try using the methods outlined above. First, we notice that the coeficients of 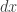 and
and 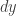 are both homogeneous of order 2, so we can make the substitution
are both homogeneous of order 2, so we can make the substitution  or
or  and the equation would become seperable. If I were doing this by hand or for a homework assignment, I would make one of those substitutions and work it through, but we have the exact form above, so let’s use it just like SymPy would.
and the equation would become seperable. If I were doing this by hand or for a homework assignment, I would make one of those substitutions and work it through, but we have the exact form above, so let’s use it just like SymPy would. 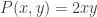 and
and 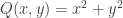 . So we get
. So we get  with
with 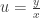 and
and  with
with  (here and for the remainder of this derivation, the arbitrary constants in the two equations do not necessarily equal each other until the last step). Both integrals can be solved with a substitution of the denominator, giving, with
(here and for the remainder of this derivation, the arbitrary constants in the two equations do not necessarily equal each other until the last step). Both integrals can be solved with a substitution of the denominator, giving, with  back substituted,
back substituted, 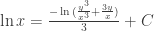 and
and 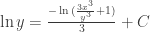 . If we make
. If we make 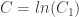 , and pull the constants in front of the logs on the right hand sides in as powers, we can combine everything into logarithms. After doing that, we then take the antilog of both sides and get
, and pull the constants in front of the logs on the right hand sides in as powers, we can combine everything into logarithms. After doing that, we then take the antilog of both sides and get 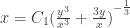 and
and 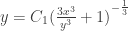 . We then raise the whole equation to the
. We then raise the whole equation to the 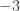 power and make
power and make  . We get
. We get
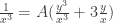
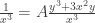
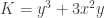
and
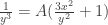

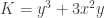 ,
,
where 
Verify as an exercise that you get the same solution by the exact differential equation methods (or don’t… you know, depending on which you’d rather do).
Of course, if that was all there was to it, I would have finished in a day. There was more. First, I had to write a function that determines if an expression is homogeneous and what order if it is. That was about 150 lines of code right there plus tests (150 lines is a lot in Python).
I also wanted it to recognize that 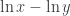 is homogeneous because
is homogeneous because  . SymPy was incapable of combining logarithms like this, so I had to write a logcombine function, which was another 100 lines of code plus tests. This came in handy, because I was also able to use it in the part above where I combined the logarithms of my answer to eliminate all of them.
. SymPy was incapable of combining logarithms like this, so I had to write a logcombine function, which was another 100 lines of code plus tests. This came in handy, because I was also able to use it in the part above where I combined the logarithms of my answer to eliminate all of them.
Lastly, you may have noticed that my math looks much nicer in this post. It turns out that WordPress supports math using $ Read the rest of this entry »
, such as
but the matching engine cannot get things like
, because it doesn’t know how to factor out the
. There is a function, collect, that can factor out expressions if you give them to it explicily with
and
.



 Posted by Aaron Meurer
Posted by Aaron Meurer  where
where . If this condition holds, then there exists a function
. If this condition holds, then there exists a function , often called a ‘potential function’ because of some applications of theses equations to physics, such that
, often called a ‘potential function’ because of some applications of theses equations to physics, such that and
and . This is because mixed partials are equal for continuous functions. The solution will then just be
. This is because mixed partials are equal for continuous functions. The solution will then just be . The tricky part is finding the potential function
. The tricky part is finding the potential function . There is a restriction where the rectangle connecting
. There is a restriction where the rectangle connecting ,
, ,
, , and
, and has to lie entirely in the domain of
has to lie entirely in the domain of  and
and , but if we let
, but if we let , then this is not really a problem for functions that SymPy will encounter. UPDATE: It turns out this is a problem if the equation has singularities in it. Fortunately, I was able to code up a workaround that usually works.
, then this is not really a problem for functions that SymPy will encounter. UPDATE: It turns out this is a problem if the equation has singularities in it. Fortunately, I was able to code up a workaround that usually works. and
and . It is much simpler for a human being to do that than the above integral, because the integral involves evaluating limits and so on, but for a computer algebra system, the above integral is a one-liner.
. It is much simpler for a human being to do that than the above integral, because the integral involves evaluating limits and so on, but for a computer algebra system, the above integral is a one-liner.