Modifying a list while looping through it in Python

Here is an interesting thing that I found. x is a SymPy Symbol:

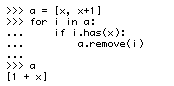
I would have expected to get a = [], but it only removes the first item. And yes, x + 1 passes the condition:

>>> (x + 1).has(x)
True


Clearly, it is a bad idea to modify a list while I am looping through it. I should instead be doing something like this:

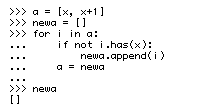
But I am intrigued as to why exactly this fails. If any of the readers of the blog thinks that he know, please post in the comments. Or, if I figure it out, I will post an update. Also, here is a similar example, with a strange result:

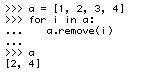
(Sorry for the images by the way. WordPress’s so called “code” blocks are impervious to indentation.)

UPDATE (a few minutes later):
Well, I figured it would come to me as to why this was happening, and it didn’t take long. While I haven’t read the actual Python Language Reference, this is what I am assuming is happening. This is all just my guessing on how Python is implemented. Please correct me if I am wrong.

So, obviously, a Python list is just a C array. It is probably an array of pointers, which is the only way I can see that would let it be mutable with different objects (this is how compiled languages with dynamic typing like Objective-C more or less pull it off). Now C does not have the for i in list syntax that Python has (nor does any other language that I know of. That is one of the reasons that Python is so awesome!), so if you want to recurse a list (C array), you have to do the usual for (i=0; i<=len(list); i++) { from C (or it probably uses a while loop, which would allow for things like iterators, but a for loop in C is literally just a wrapper around a while loop anyway). Then of course, inside of the loop, you just have list[i] blocks. So when I was going through my list, for example, the list of numbers in the last example, it would hit item 0 (the first item), remove it, which would amount to rebuilding the list as [2, 3, 4, 5], then it would hit item 1, which is now 3, remove it, rebuilding the list, and so on. So the even numbered elements remain because it skips every element after one that it removes. CPython must have good error handling, because eventually this would cause the indices to go beyond the length of the list. It seems to me that this behavior is not very well defined. Personally, I think that whatever you are looping through in a for loop should become immutable within the loop block. I checked Python 3.1, and the behavior is exactly the same.

Based on this, .remove() rebuilds the list each time. I would have thought it would just set the value in the array to Null, but I guess that would make it more difficult to test equality with an equivalent list that doesn’t have Null values. It is good to know that .remove() does that, because it means that can be an expensive operation.

Constant stuff

So I was able to get a working version of the Constant class, but because the code cluttered up the internal Add and Mul classes too much, Ondrej convinced me that to make a function that does the simplification instead, and I reluctantly agreed. After begining work on it, I realized that it will be much easier to make it just an internal function that handles the special cases presented by dsolve(). That means that it will only handle arbitrary constants that are independent of one variable, and it will only work with constants that are named as “C1”, “C2”, and so on.

If we ever get the sympyx core that Ondrej and I worked on when I was in Los Alamos in, it will be easy for my to use a Constant class, because it will have handler logic that will allow for the Constant class to exist independent of Add and Mul. It already can exist independent of Pow with a minor code addition, but simplifying powers is easier than simplifying addition and multiplcation because exponentiation is neither commutative nor associative, meaning that you don’t have to worry about absorbing stuff on the other side of something, like 2 + x + C.

See my constant-Mul branch for my working version of a Constant class the implements in Mul and Add. See my constant-function branch for my work on the internal function.

Because I have decided to make thing simple and make the function internal only, I should have things up and running soon. Then, it will be simple to fix up my nth order homogeneous stuff that I already have so that it works, and then to implement variation of parameters!

Meeting Ondrej in Los Alamos

So Ondrej was kind enough to have me over to his house in Los Alamos for Friday and Saturday. We spent a lot of time coding together. While we worked on some other things too, we mainly worked on my constant class. Ondrej and I came up with an idea for restructured Mul and Add classes that would allow different objects in them to handle the other objects in them. The way it is now, if I want my Constant object to absorb other objects, like 2*a*C*x => C*x, I have to hardcode it into Mul. The same is true with Add. This makes the Mul and Add classes muddy. Right now, there is already special handling for other such dynamic objects such as Order classes (e.g., O(x)), and Infinity class. See the Add.flatten() and Mul.flatten() methods in sympy/core/add.py and sympy.core/mul.py to see what I mean.

We came up with a system where symbols and numbers are handled the same way, because we need them to be fast, but if an expression has an object that has a handle_mul() method, it will call that method with the other objects in the expression in the Mul/Add and the object will take care of the special handling. Ondrej was able to get most of it working in his experimental core that doesn’t use assumptions here. We will hopefully end up using it, but we need to wait until we merge the new assumptions system.

So in the mean while, I have a working Constant class that modifies Mul and Add here. Since it will take a while until the new assumptions system is done (Fabian Seoane is doing it for his Google Summer of Code project), we may end up temporarily adding in my Constant branch. Once I have a working Constant class, I can solve homogeneous differential equations (not to be confused with first order differential equations with homogeneous coefficients) with one case (there are several cases depending on whether the roots of the so called characteristic equation are real, imaginary, or complex, but we can actually handle them in one case if we have constants that combine into each other. More on this in a later post). Once I have that (which I have everything already except for the arbitrary constants), I can then implement variation of parameters, which, along with separable, will probably be the most used solver of the ones that I will implement this summer.

Once I get those, I can clean up a lot of the 2nd order differential equation code in dsolve (currently it is just a hack with a bunch of special cases all covered by variation of parameters). With that code cleaned up, I can refactor dsolve to use my proposed hints engine, which will allow the user to choose which methods they want to use to solve an equation (more on that in a later post too).

Update

It’s been a while since I’ve posted here, so I figured an update was in order. Here is a list of stuff that I have done since my last post.

– I recovered my data from my Terminal history. This wasn’t too difficult as I predicted. I just had to do some minor formatting on the git commit --interactive data to make it a valid git patch file. For whatever reason, a handful of the changes wouldn’t apply because git couldn’t find where changed lines were, even though they were identical to what was in the patch. git apply doesn’t seem to have a merge option, but eventually I found the --reject option, which puts failed patches in .rej files, instead of just failing the whole apply.

– I got separable equations implemented in dsolve. I actually did this on the road before I lost my data, but I failed to mention it before, so here it is. The hardest part with that was creating a decent separatevars() function that could separate just about any funciton. As I mentioned in an earlier post, this involved changing the way that SymPy handles automatic combining of exponents in the core, as well as refactoring expand. I also had to make the function completely independent of match, because match is too buggy to work correctly for separable equations.

– Speaking of refactoring expand and combining exponents, that work made it in! It is the first major thing that I have done that has actually made it into the main SymPy repo. It got in just before the release of SymPy 0.6.5-beta2, so it should be in the final release of SymPy 0.6.5. Most likely, none of my ODE stuff will make it in until 0.7.

– I started to work on Variation of Parameters, but before I could actually get to the variation of parameters part, I needed to be able to solve a homogeneous equation ( constant for all ). If you know how that works, it involves finding the roots of the polynomial given by . Depending on whether these roots are real, imaginary, or complex, you have different solutions with exponentials or sin’s and cos’s. I had no trouble getting the exponentials and the sin’s and cos’s to work correctly (SymPy already has a root finder that I put to work), but I did have a problem getting the arbitrary constants to work correcty. It turns out that the code for that would be much simpler if I had an arbitrary constant type that automatically “absorbed” other constants. Since I had planned on doing that anyway, I decided to put the rest of variation of parameters on hold and begin work on that.

– We had a Documentation day on June 30, and I decided to write up a document that would help people new to SymPy and Python with some of the gotchas and pitfalls. For example, unlike most other independent CAS’s like Maple, you can’t just type 1/2 in SymPy to get . That is because Python evaluates it numerically. You have to do S(1)/2 or Rational(1,2) to get the Rational class. It’s all things like that. It’s taken me a while to get it together, not because it took me long to write it, but because it has to be in the Sphinx documentation format, which I have had to learn. I am just finishing it up now.

– I met with Ondrej on Saturday. He went down from Los Alamos to Carlsbad with a friend to see the caverns, and they stopped here in Albuquerque on the way back up. He came just in time to see the fireworks, and after that got some dinner. We weren’t able to do any coding, but hopefully we will be able to meet up again later this summer to do some of that.